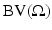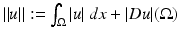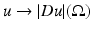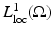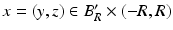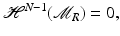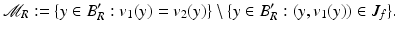(1)
where
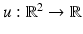 denotes the ideal undistorted image,
denotes the ideal undistorted image, 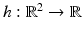 is a blurring kernel, f is the observed image which is represented as a function
is a blurring kernel, f is the observed image which is represented as a function 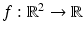 , and n is an additive white noise with zero mean and standard deviation σ. In practice, the noise can be considered as Gaussian.
, and n is an additive white noise with zero mean and standard deviation σ. In practice, the noise can be considered as Gaussian.A particular and important case contained in the above formulation is the denoising problem which corresponds to the case where h = δ, so that Eq. (1) is written as
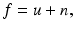
where n is an additive Gaussian white noise of zero mean and variance σ 2.
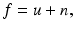
(2)
The problem of recovering u from f is ill-posed. Several methods have been proposed to recover u. Most of them can be classified as regularization methods which may take into account statistical properties (Wiener filters), information theoretic properties [35], a priori geometric models [55], or the functional analytic behavior of the image given in terms of its wavelet coefficients (see [48] and references therein).
The typical strategy to solve this ill-conditioning is regularization [56]. In the linear case the solution of (1) is estimated by minimizing a functional
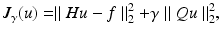
which yields the estimate
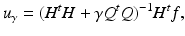
where 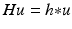 , and Q is a regularization operator. Observe that to obtain u γ we have to solve a system of linear equations. The role of Q is, on one hand, to move the small eigenvalues of H away from zero while leaving the large eigenvalues unchanged, and, on the other hand, to incorporate the a priori (smoothness) knowledge that we have on u.
, and Q is a regularization operator. Observe that to obtain u γ we have to solve a system of linear equations. The role of Q is, on one hand, to move the small eigenvalues of H away from zero while leaving the large eigenvalues unchanged, and, on the other hand, to incorporate the a priori (smoothness) knowledge that we have on u.
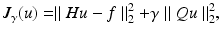
(3)
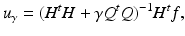
(4)
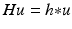 , and Q is a regularization operator. Observe that to obtain u γ we have to solve a system of linear equations. The role of Q is, on one hand, to move the small eigenvalues of H away from zero while leaving the large eigenvalues unchanged, and, on the other hand, to incorporate the a priori (smoothness) knowledge that we have on u.
, and Q is a regularization operator. Observe that to obtain u γ we have to solve a system of linear equations. The role of Q is, on one hand, to move the small eigenvalues of H away from zero while leaving the large eigenvalues unchanged, and, on the other hand, to incorporate the a priori (smoothness) knowledge that we have on u.If we treat u and n as random vectors and we select γ = 1 and 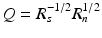 with R s and R n the image and noise covariance matrices, then (4) corresponds to the Wiener filter that minimizes the mean square error between the original and restored images.
with R s and R n the image and noise covariance matrices, then (4) corresponds to the Wiener filter that minimizes the mean square error between the original and restored images.
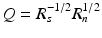 with R s and R n the image and noise covariance matrices, then (4) corresponds to the Wiener filter that minimizes the mean square error between the original and restored images.
with R s and R n the image and noise covariance matrices, then (4) corresponds to the Wiener filter that minimizes the mean square error between the original and restored images.One of the first regularization methods consisted in choosing between all possible solutions of (1) the one which minimized the Sobolev (semi) norm of u
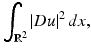
which corresponds to the case Qu = Du. In the Fourier domain the solution of (3) given by (4) is 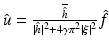 . From the above formula we see that high frequencies of f (hence, the noise) are attenuated by the smoothness constraint.
. From the above formula we see that high frequencies of f (hence, the noise) are attenuated by the smoothness constraint.
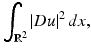
(5)
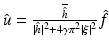 . From the above formula we see that high frequencies of f (hence, the noise) are attenuated by the smoothness constraint.
. From the above formula we see that high frequencies of f (hence, the noise) are attenuated by the smoothness constraint.This formulation was an important step, but the results were not satisfactory, mainly due to the inability of the previous functional to resolve discontinuities (edges) and oscillatory textured patterns. The smoothness required by the finiteness of the Dirichlet integral (5) constraint is too restrictive. Indeed, functions in 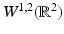 (i.e., functions
(i.e., functions 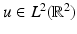 such that
such that 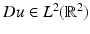 ) cannot have discontinuities along rectifiable curves. These observations motivated the introduction of Total Variation in image restoration problems by L. Rudin, S. Osher, and E. Fatemi in their work [55]. The a priori hypothesis is that functions of bounded variation (the BV model) [9] are a reasonable functional model for many problems in image processing, in particular, for restoration problems [55]. Typically, functions of bounded variation have discontinuities along rectifiable curves, being continuous in some sense (in the measure theoretic sense) away from discontinuities [9]. The discontinuities could be identified with edges. The ability of total variation regularization to recover edges is one of the main features which advocates for the use of this model, but its ability to describe textures is less clear, even if some textures can be recovered, up to a certain scale of oscillation. An interesting experimental discussion of the adequacy of the BV -model to describe real images can be found in [41].
) cannot have discontinuities along rectifiable curves. These observations motivated the introduction of Total Variation in image restoration problems by L. Rudin, S. Osher, and E. Fatemi in their work [55]. The a priori hypothesis is that functions of bounded variation (the BV model) [9] are a reasonable functional model for many problems in image processing, in particular, for restoration problems [55]. Typically, functions of bounded variation have discontinuities along rectifiable curves, being continuous in some sense (in the measure theoretic sense) away from discontinuities [9]. The discontinuities could be identified with edges. The ability of total variation regularization to recover edges is one of the main features which advocates for the use of this model, but its ability to describe textures is less clear, even if some textures can be recovered, up to a certain scale of oscillation. An interesting experimental discussion of the adequacy of the BV -model to describe real images can be found in [41].
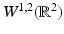 (i.e., functions
(i.e., functions 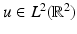 such that
such that 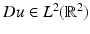 ) cannot have discontinuities along rectifiable curves. These observations motivated the introduction of Total Variation in image restoration problems by L. Rudin, S. Osher, and E. Fatemi in their work [55]. The a priori hypothesis is that functions of bounded variation (the BV model) [9] are a reasonable functional model for many problems in image processing, in particular, for restoration problems [55]. Typically, functions of bounded variation have discontinuities along rectifiable curves, being continuous in some sense (in the measure theoretic sense) away from discontinuities [9]. The discontinuities could be identified with edges. The ability of total variation regularization to recover edges is one of the main features which advocates for the use of this model, but its ability to describe textures is less clear, even if some textures can be recovered, up to a certain scale of oscillation. An interesting experimental discussion of the adequacy of the BV -model to describe real images can be found in [41].
) cannot have discontinuities along rectifiable curves. These observations motivated the introduction of Total Variation in image restoration problems by L. Rudin, S. Osher, and E. Fatemi in their work [55]. The a priori hypothesis is that functions of bounded variation (the BV model) [9] are a reasonable functional model for many problems in image processing, in particular, for restoration problems [55]. Typically, functions of bounded variation have discontinuities along rectifiable curves, being continuous in some sense (in the measure theoretic sense) away from discontinuities [9]. The discontinuities could be identified with edges. The ability of total variation regularization to recover edges is one of the main features which advocates for the use of this model, but its ability to describe textures is less clear, even if some textures can be recovered, up to a certain scale of oscillation. An interesting experimental discussion of the adequacy of the BV -model to describe real images can be found in [41].In order to work with images, we assume that they are defined in a bounded domain 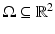 which we assume to be the interval [0, N[2. As in most of the works, in order to simplify this problem, we shall assume that the functions h and u are periodic of period N in each direction. That amounts to neglecting some boundary effects. Therefore, we shall assume that h, u are functions defined in
which we assume to be the interval [0, N[2. As in most of the works, in order to simplify this problem, we shall assume that the functions h and u are periodic of period N in each direction. That amounts to neglecting some boundary effects. Therefore, we shall assume that h, u are functions defined in 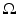 and, to fix ideas, we assume that
and, to fix ideas, we assume that 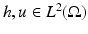 . Our problem is to recover as much as possible of u, from our knowledge of the blurring kernel h, the statistics of the noise n, and the observed image f.
. Our problem is to recover as much as possible of u, from our knowledge of the blurring kernel h, the statistics of the noise n, and the observed image f.
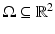 which we assume to be the interval [0, N[2. As in most of the works, in order to simplify this problem, we shall assume that the functions h and u are periodic of period N in each direction. That amounts to neglecting some boundary effects. Therefore, we shall assume that h, u are functions defined in
which we assume to be the interval [0, N[2. As in most of the works, in order to simplify this problem, we shall assume that the functions h and u are periodic of period N in each direction. That amounts to neglecting some boundary effects. Therefore, we shall assume that h, u are functions defined in 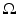 and, to fix ideas, we assume that
and, to fix ideas, we assume that 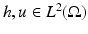 . Our problem is to recover as much as possible of u, from our knowledge of the blurring kernel h, the statistics of the noise n, and the observed image f.
. Our problem is to recover as much as possible of u, from our knowledge of the blurring kernel h, the statistics of the noise n, and the observed image f.On the basis of the BV model, Rudin–Osher–Fatemi [55] proposed to solve the following constrained minimization problem:
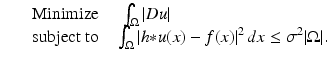
Notice that the image acquisition model (1) is only incorporated through a global constraint. Assuming that h ∗ 1 = 1 (energy preservation), the additional constraint that 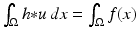 is automatically satisfied by its minima [28]. In practice, the above problem is solved via the following unconstrained minimization problem:
is automatically satisfied by its minima [28]. In practice, the above problem is solved via the following unconstrained minimization problem:
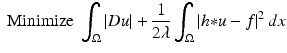
where the parameter λ is positive. Recall that we may interpret λ as a penalization parameter which controls the trade-off between the goodness of fit of the constraint and the smoothness term given by the Total Variation. In this formulation, a methodology is required for a correct choice of λ. The connections between (6) and (7) were studied by A. Chambolle and P.L. Lions in [28] where they proved that both problems are equivalent for some positive value of the Lagrange multiplier λ.
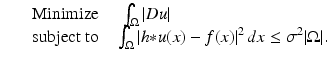
(6)
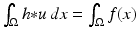 is automatically satisfied by its minima [28]. In practice, the above problem is solved via the following unconstrained minimization problem:
is automatically satisfied by its minima [28]. In practice, the above problem is solved via the following unconstrained minimization problem: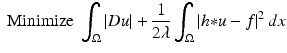
(7)
In the denoising case, the unconstrained variational formulation (7) with h = δ is
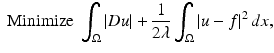
and it has been the object of much theoretical and numerical research (see [10, 56] for a survey). Even if this model represented a theoretical and practical progress in the denoising problem due to the introduction of BV functions as image models, the experimental analysis readily showed its main drawbacks. Between them, let us mention the staircasing effect (when denoising a smooth ramp plus noise, the staircase is an admissible result), the pixelization of the image at smooth regions, and the loss of fine textured regions, to mention some of them. This can be summarized with the simple observation that the residuals f − u, where u represents the solution of (8), do not look like noise. This has motivated the development of nonlocal filters [17] for denoising, the use of a stochastic optimization technique to estimate u [47], or the consideration of the image acquisition model as a set of local constraints [3, 38] to be discussed below.
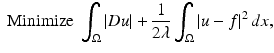
(8)
Let us finally mention that, following the analysis of Y. Meyer in [48], the solution u of (8) permits to obtain a decomposition of the data f as a sum of two components u + v where u contains the geometric sketch of f while v is supposed to contain its noise and textured parts.As Meyer observed, the L 2 norm of the residual v: = f − u in (8) is not the right one to obtain a decomposition of f in terms of geometry plus texture and he proposed to measure the size of the textured part v in terms of a dual BV norm showing that some models of texture have indeed a small dual BV norm.
In spite of its limitations, the total variation model has become one of the basic image models and has been adapted to many tasks: optical flow, stereo imaging and 3D surface reconstruction, segmentation, interpolation, or the study of u + v models to mention a few cases. On the other hand, when compared to other robust regularization terms, it combines simplicity and geometric character and makes it possible a rigorous analysis. The theoretical analysis of the behavior of solutions of (8) has been the object of several works [6, 13, 14, 20, 48, 50] and will be summarized in Sects. 3 and 4.
Recall that one of the main reasons to introduce the Total Variation as a regularization term in imaging problems was its ability to recover discontinuities in the solution. This intuition has been confirmed by the experimental evidence and has been the motivation for the study of the local regularity properties of (8) in [20, 23]. After recalling in Sect. 2 some basic notions and results in the theory of bounded variation functions, we prove in section “The Discontinuities of Solutions of the TV Denoising Problem” that the set of jumps (in the BV sense) of the solution of (8) is contained in the set of jumps of the datum f [20]. In other words, model (8) does not create any new discontinuity besides the existing ones. As a refinement of the above statement, the local Hölder regularity of the solutions of (8) is studied in section “Hölder Regularity Results.” This has to be combined with results describing which discontinuities are preserved. No general statement in this sense exists, but many examples are described in the papers [5, 10, 13, 14]. The preservation of a jump discontinuity depends on the curvature of the level line at the given point, the size of the jump, and the regularization parameter λ. This is illustrated in the example given in Sect. 4. The examples support the idea that total variation is not perfect but may be a reasonable regularization term in order to restore discontinuities.
Being considered as a basic model, the numerical analysis of the total variation model has been the object of intensive research. Many numerical approaches have been proposed in order to give fast, efficient methods which are also versatile to cover the whole range of applications. In Sect. 5 we review some basic iterative methods introduced to solve the Euler–Lagrange equations of (8). In particular, we review in section “Chambolle’s Algorithm” the dual approach introduced by A. Chambolle in [25]. In section “Primal-Dual Approaches” we review the primal-dual scheme of Zhu and Chan [57]. Both of them are between the most popular schemes by now. In Sect. 6 we discuss global optimization methods based on graph-cut techniques adapted to solve a quantized version of (8). Those methods have also become very popular due to its efficiency and versatility in applications and are an active area of research, as it can be seen in the references. Then, in section “Global Solutions of Geometric Problems” we review the applications of anisotropic TV problems to find the global solution of geometric problems. Similar anisotropic TV formulations appear as convexifications of nonlinear energies for disparity computation in stereo imaging, or related problems [30, 52], and they are reviewed in section “A Convex Formulation of Continuous Multilabel Problems.”
In Sect. 8 we review the application of Total Variation in image restoration (6), describing the approach where the image acquisition model is introduced as a set of local constraints [3, 38, 54].
We could not close this chapter without reviewing in Sect. 9 a recent algorithm introduced by C. Louchet and L. Moisan [47] which uses a Bayesian approach leading to an estimate of u as the expected value of the posterior distribution of u given the data f. This estimate requires to compute an integral in a high dimensional space and the authors use a Monte-Carlo method with Markov Chain (MCMC) [47]. In this context, the minimization of the discrete version of (8) corresponds to a Maximum a Posterior (MAP) estimate of u.
2 Notation and Preliminaries on BV Functions
Definition and Basic Properties
Let 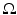 be an open subset of
be an open subset of 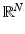 . Let
. Let 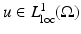 . Recall that the distributional gradient of u is defined by
. Recall that the distributional gradient of u is defined by
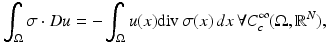 where
where 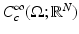 denotes the vector fields with values in
denotes the vector fields with values in 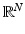 which are infinitely differentiable and have compact support in
which are infinitely differentiable and have compact support in 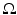 . The total variation of
. The total variation of 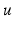 in
in 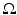 is defined by
is defined by
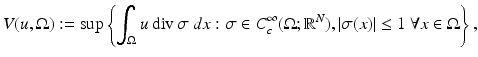
where for a vector 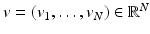 we set
we set 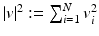 . Following the usual notation, we will denote
. Following the usual notation, we will denote 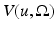 by
by 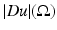 or by
or by 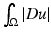 .
.
 be an open subset of
be an open subset of 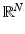 . Let
. Let 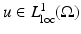 . Recall that the distributional gradient of u is defined by
. Recall that the distributional gradient of u is defined by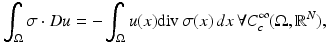
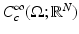 denotes the vector fields with values in
denotes the vector fields with values in 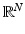 which are infinitely differentiable and have compact support in
which are infinitely differentiable and have compact support in  . The total variation of
. The total variation of 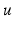 in
in  is defined by
is defined by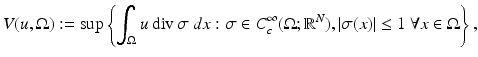
(9)
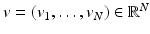 we set
we set 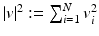 . Following the usual notation, we will denote
. Following the usual notation, we will denote 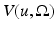 by
by 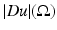 or by
or by 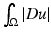 .
.Definition 1.
Let 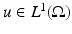 . We say that u is a function of bounded variation in
. We say that u is a function of bounded variation in 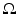 if
if 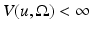 . The vector space of functions of bounded variation in
. The vector space of functions of bounded variation in 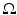 will be denoted by
will be denoted by 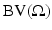 .
.
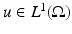 . We say that u is a function of bounded variation in
. We say that u is a function of bounded variation in 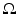 if
if 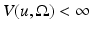 . The vector space of functions of bounded variation in
. The vector space of functions of bounded variation in 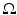 will be denoted by
will be denoted by 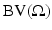 .
.Using Riesz representation Theorem [9], the above definition can be rephrased by saying that u is a function of bounded variation in 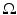 if the gradient Du in the sense of distributions is a (vector valued) Radon measure with finite total variation
if the gradient Du in the sense of distributions is a (vector valued) Radon measure with finite total variation 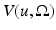 .
.
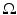 if the gradient Du in the sense of distributions is a (vector valued) Radon measure with finite total variation
if the gradient Du in the sense of distributions is a (vector valued) Radon measure with finite total variation 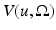 .
.Sets of Finite Perimeter: The Co-area Formula
Definition 2.
A measurable set 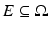 is said to be of finite perimeter in
is said to be of finite perimeter in 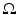 if
if 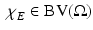 . The perimeter of E in
. The perimeter of E in 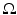 is defined as
is defined as 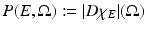 . If
. If 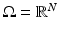 , we denote the perimeter of E in
, we denote the perimeter of E in 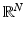 by P(E).
by P(E).
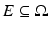 is said to be of finite perimeter in
is said to be of finite perimeter in 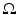 if
if 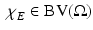 . The perimeter of E in
. The perimeter of E in 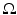 is defined as
is defined as 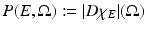 . If
. If 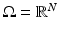 , we denote the perimeter of E in
, we denote the perimeter of E in 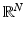 by P(E).
by P(E).The following inequality holds for any two sets 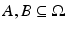 :
:
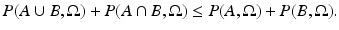
 :
: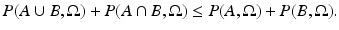
(10)
Theorem 1.
Let 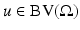 . Then for a.e.
. Then for a.e.  the set {u > t} is of finite perimeter in
the set {u > t} is of finite perimeter in  and one has
and one has
![$$\displaystyle{\int _{\Omega }\vert Du\vert =\int _{ -\infty }^{\infty }P(\{u > t\},\Omega )\,dt.}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_Equb.gif”></DIV></DIV></DIV><SPAN class=EmphasisTypeItalic>In other words, the total variation of u amounts to the sum of the perimeters of its upper level sets.</SPAN> </DIV></DIV><br />
<DIV class=Para>An analogous formula with the lower level sets is also true. For a proof we refer to [<CITE><A href=]() 9].
9].
![$$\displaystyle{\int _{\Omega }\vert Du\vert + \frac{1} {2\lambda }\int _{\Omega }(u - f)^{2}\,dx =\int _{ \mathbb{R}}\left (P\left (\{u > t\},\Omega \right ) + \frac{1} {\lambda } \int _{\{u>t\}}(t – f)\,dx\right )dt\,,}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_Equf.gif”></DIV></DIV></DIV>and from the following comparison result for solutions of (<SPAN class=InternalRef><A href=]() 14) which is proved in [5, Lemma 4]:
14) which is proved in [5, Lemma 4]:
Get Clinical Tree app for offline access

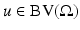 . Then for a.e.
. Then for a.e.  the set {u > t} is of finite perimeter in
the set {u > t} is of finite perimeter in 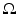 and one has
and one hasThe Structure of the Derivative of a BV Function
Let us denote by 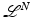 and
and 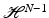 , respectively, the N-dimensional Lebesgue measure and the (N − 1)-dimensional Hausdorff measure in
, respectively, the N-dimensional Lebesgue measure and the (N − 1)-dimensional Hausdorff measure in 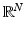 (see [9] for precise definitions).
(see [9] for precise definitions).
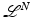 and
and 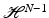 , respectively, the N-dimensional Lebesgue measure and the (N − 1)-dimensional Hausdorff measure in
, respectively, the N-dimensional Lebesgue measure and the (N − 1)-dimensional Hausdorff measure in 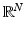 (see [9] for precise definitions).
(see [9] for precise definitions).Let ![$$u \in [L_{{\mathrm{loc}}}^{1}(\Omega )]^{m}$$](/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_IEq52.gif) (m ≥ 1). We say that u has an approximate limit at
(m ≥ 1). We say that u has an approximate limit at 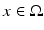 if there exists
if there exists 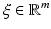 such that
such that
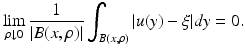
The set of points where this does not hold is called the approximate discontinuity set of u, and is denoted by S u . Using Lebesgue’s differentiation theorem, one can show that the approximate limit ξ exists at 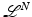 -a.e.
-a.e. 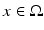 , and is equal to u(x), in particular, | S u | = 0. If
, and is equal to u(x), in particular, | S u | = 0. If 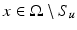 , the vector ξ is uniquely determined by (11) and we denote it by
, the vector ξ is uniquely determined by (11) and we denote it by 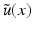 .
.
![$$u \in [L_{{\mathrm{loc}}}^{1}(\Omega )]^{m}$$](/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_IEq52.gif) (m ≥ 1). We say that u has an approximate limit at
(m ≥ 1). We say that u has an approximate limit at 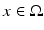 if there exists
if there exists 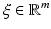 such that
such that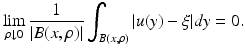
(11)
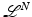 -a.e.
-a.e. 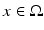 , and is equal to u(x), in particular, | S u | = 0. If
, and is equal to u(x), in particular, | S u | = 0. If 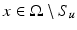 , the vector ξ is uniquely determined by (11) and we denote it by
, the vector ξ is uniquely determined by (11) and we denote it by 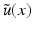 .
.We say that u is approximately continuous at x if 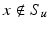 and
and 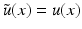 , that is, if x is a Lebesgue point of u (with respect to the Lebesgue measure).
, that is, if x is a Lebesgue point of u (with respect to the Lebesgue measure).
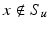 and
and 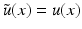 , that is, if x is a Lebesgue point of u (with respect to the Lebesgue measure).
, that is, if x is a Lebesgue point of u (with respect to the Lebesgue measure).Let ![$$u \in [L_{{\mathrm{loc}}}^{1}(\Omega )]^{m}$$](/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_IEq61.gif) and
and 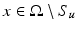 ; we say that u is approximately differentiable at x if there exists an m × N matrix L such that
; we say that u is approximately differentiable at x if there exists an m × N matrix L such that
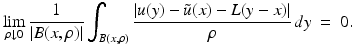
In that case, the matrix L is uniquely determined by (12) and is called the approximate differential of u at x.
![$$u \in [L_{{\mathrm{loc}}}^{1}(\Omega )]^{m}$$](/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_IEq61.gif) and
and 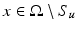 ; we say that u is approximately differentiable at x if there exists an m × N matrix L such that
; we say that u is approximately differentiable at x if there exists an m × N matrix L such that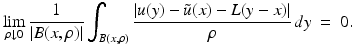
(12)
For 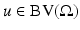 , the gradient Du is a N-dimensional Radon measure that decomposes into its absolutely continuous and singular parts Du = D a u + D s u. Then D a u = ∇u dx where ∇u is the Radon–Nikodym derivative of the measure
, the gradient Du is a N-dimensional Radon measure that decomposes into its absolutely continuous and singular parts Du = D a u + D s u. Then D a u = ∇u dx where ∇u is the Radon–Nikodym derivative of the measure 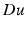 with respect to the Lebesgue measure in
with respect to the Lebesgue measure in 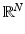 . The function u is approximately differentiable
. The function u is approximately differentiable 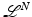 -a.e. in
-a.e. in 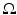 and the approximate differential coincides with
and the approximate differential coincides with 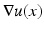
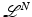 -a.e. The singular part D s u can be also split into two parts: the jump part D j u and the Cantor part D c u.
-a.e. The singular part D s u can be also split into two parts: the jump part D j u and the Cantor part D c u.
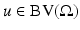 , the gradient Du is a N-dimensional Radon measure that decomposes into its absolutely continuous and singular parts Du = D a u + D s u. Then D a u = ∇u dx where ∇u is the Radon–Nikodym derivative of the measure
, the gradient Du is a N-dimensional Radon measure that decomposes into its absolutely continuous and singular parts Du = D a u + D s u. Then D a u = ∇u dx where ∇u is the Radon–Nikodym derivative of the measure 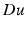 with respect to the Lebesgue measure in
with respect to the Lebesgue measure in 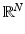 . The function u is approximately differentiable
. The function u is approximately differentiable 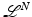 -a.e. in
-a.e. in 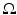 and the approximate differential coincides with
and the approximate differential coincides with 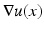
 -a.e. The singular part D s u can be also split into two parts: the jump part D j u and the Cantor part D c u.
-a.e. The singular part D s u can be also split into two parts: the jump part D j u and the Cantor part D c u.We say that  is an approximate jump point of u if there exist
is an approximate jump point of u if there exist 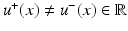 and
and 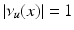 such that
such that
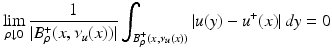
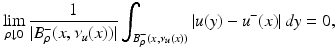 where
where 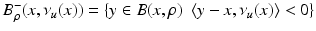 . We denote by J u the set of approximate jump points of u. If
. We denote by J u the set of approximate jump points of u. If 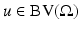 , the set S u is countably
, the set S u is countably 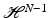 rectifiable, J u is a Borel subset of S u , and
rectifiable, J u is a Borel subset of S u , and 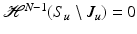 [9]. In particular, we have that
[9]. In particular, we have that 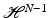 -a.e.
-a.e. 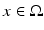 is either a point of approximate continuity of
is either a point of approximate continuity of 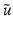 or a jump point with two limits in the above sense. Finally, we have
or a jump point with two limits in the above sense. Finally, we have
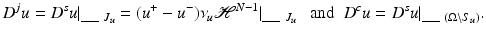
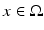 is an approximate jump point of u if there exist
is an approximate jump point of u if there exist 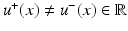 and
and 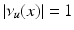 such that
such that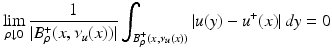
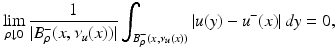
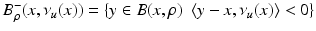 . We denote by J u the set of approximate jump points of u. If
. We denote by J u the set of approximate jump points of u. If 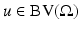 , the set S u is countably
, the set S u is countably  rectifiable, J u is a Borel subset of S u , and
rectifiable, J u is a Borel subset of S u , and 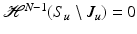 [9]. In particular, we have that
[9]. In particular, we have that 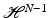 -a.e.
-a.e. 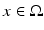 is either a point of approximate continuity of
is either a point of approximate continuity of 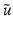 or a jump point with two limits in the above sense. Finally, we have
or a jump point with two limits in the above sense. Finally, we have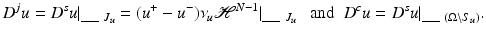
For a comprehensive treatment of functions of bounded variation we refer to [9].
3 The Regularity of Solutions of the TV Denoising Problem
The Discontinuities of Solutions of the TV Denoising Problem
Given a function 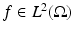 and λ > 0 we consider the minimum problem
and λ > 0 we consider the minimum problem
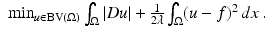
Notice that problem (13) always admits a unique solution u λ , since the energy functional is strictly convex.
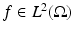 and λ > 0 we consider the minimum problem
and λ > 0 we consider the minimum problem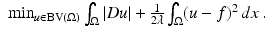
(13)
As we mentioned in Sect. 1, one of the main reasons to introduce the Total Variation as a regularization term in imaging problems was its ability to recover the discontinuities in the solution. This section together with section “Hölder Regularity Results” and Sect. 4 is devoted to analyze this assertion. In this section we prove that the set of jumps of u λ (in the BV sense) is contained in the set of jumps of f, whenever f has bounded variation. Thus, model (13) does not create any new discontinuity besides the existing ones. Section “Hölder Regularity Results” is devoted to review a local Hölder regularity result of [23]: the local Hol̈der regularity of the data is inherited by the solution. This has to be combined with results describing which discontinuities are preserved. In Sect. 4 we give an example of explicit solution of (13) which shows that the preservation of a jump discontinuity depends on the curvature of the level line at the given point, the size of the jump, and the regularization parameter λ. Other examples are given in the papers [2, 5, 10, 13, 14]. The examples support the idea that total variation may be a reasonable regularization term in order to restore discontinuities.
Proposition 1.
Let u λ be the (unique) solution of (13) . Then, for any 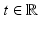 , {u λ > t} (respectively, {u λ ≥ t}) is the minimal (resp., maximal) solution of the minimal surface problem
, {u λ > t} (respectively, {u λ ≥ t}) is the minimal (resp., maximal) solution of the minimal surface problem
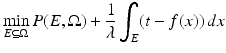
(whose solution is defined in the class of finite-perimeter sets, hence up to a Lebesgue-negligible set). In particular, for all 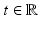 but a countable set, {u λ = t} has zero measure and the solution of (14) is unique up to a negligible set.
but a countable set, {u λ = t} has zero measure and the solution of (14) is unique up to a negligible set.
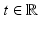 , {u λ > t} (respectively, {u λ ≥ t}) is the minimal (resp., maximal) solution of the minimal surface problem
, {u λ > t} (respectively, {u λ ≥ t}) is the minimal (resp., maximal) solution of the minimal surface problem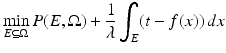
(14)
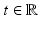 but a countable set, {u λ = t} has zero measure and the solution of (14) is unique up to a negligible set.
but a countable set, {u λ = t} has zero measure and the solution of (14) is unique up to a negligible set. A proof that {u λ > t} and {u λ ≥ t} both solve (14) is found in [24, Prop. 2.2]. A complete proof of this proposition, which we do not give here, follows from the co-area formula, which shows that, up to a renormalization, for any 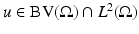 ,
,
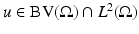 ,
,Lemma 1.
Let 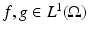 and E and F be respectively minimizers of
and E and F be respectively minimizers of
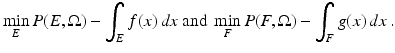 Then, if f < g a.e.,
Then, if f < g a.e., 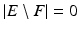 (in other words, E ⊆ F up to a negligible set).
(in other words, E ⊆ F up to a negligible set).
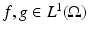 and E and F be respectively minimizers of
and E and F be respectively minimizers of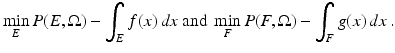
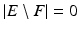 (in other words, E ⊆ F up to a negligible set).
(in other words, E ⊆ F up to a negligible set). Proof.
Observe that we have
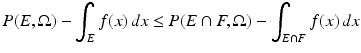
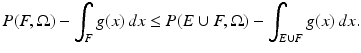 Adding both inequalities and using that for two sets of finite perimeter we have (10)
Adding both inequalities and using that for two sets of finite perimeter we have (10) 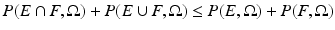 , we obtain that
, we obtain that
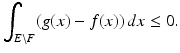 Since g(x) − f(x) > 0 a.e., this implies that
Since g(x) − f(x) > 0 a.e., this implies that 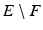 is a null set. □
is a null set. □
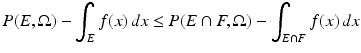
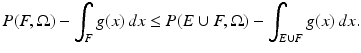
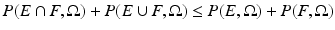 , we obtain that
, we obtain that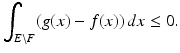
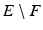 is a null set. □
is a null set. □ The proof of this last lemma is easily generalized to other situations (Dirichlet boundary conditions, anisotropic and/or nonlocal perimeters; see [5] and also [2] for a similar general statement). Eventually, we mention that the result of Proposition 1 remains true if the term (u(x) − f(x))2∕(2λ) in (13) is replaced with a term of the form 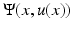 , with
, with 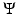 of class C 1 and strictly convex in the second variable, and replacing (t − f(x))∕λ with
of class C 1 and strictly convex in the second variable, and replacing (t − f(x))∕λ with 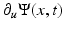 in (14).
in (14).
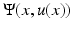 , with
, with 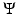 of class C 1 and strictly convex in the second variable, and replacing (t − f(x))∕λ with
of class C 1 and strictly convex in the second variable, and replacing (t − f(x))∕λ with 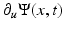 in (14).
in (14).From Proposition 1 and the regularity theory for surfaces of prescribed curvature (see for instance [8]), we obtain the following regularity result (see also [2]).
Corollary 1.
Let 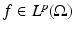 , with p > N. Then, for all
, with p > N. Then, for all 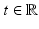 the super-level set E t: ={ u λ > t} (respectively, {u λ ≥ t}) has boundary of class C 1,α, for all α < (p − N)∕p, out of a closed singular set
the super-level set E t: ={ u λ > t} (respectively, {u λ ≥ t}) has boundary of class C 1,α, for all α < (p − N)∕p, out of a closed singular set 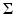 of Hausdorff dimension at most N − 8. Moreover, if p = ∞, the boundary of E t is of class W 2,q out of
of Hausdorff dimension at most N − 8. Moreover, if p = ∞, the boundary of E t is of class W 2,q out of 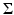 , for all q < ∞, and is of class C 1,1 if N = 2.
, for all q < ∞, and is of class C 1,1 if N = 2.
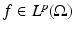 , with p > N. Then, for all
, with p > N. Then, for all 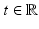 the super-level set E t: ={ u λ > t} (respectively, {u λ ≥ t}) has boundary of class C 1,α, for all α < (p − N)∕p, out of a closed singular set
the super-level set E t: ={ u λ > t} (respectively, {u λ ≥ t}) has boundary of class C 1,α, for all α < (p − N)∕p, out of a closed singular set 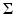 of Hausdorff dimension at most N − 8. Moreover, if p = ∞, the boundary of E t is of class W 2,q out of
of Hausdorff dimension at most N − 8. Moreover, if p = ∞, the boundary of E t is of class W 2,q out of 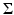 , for all q < ∞, and is of class C 1,1 if N = 2.
, for all q < ∞, and is of class C 1,1 if N = 2. We now show that the jump set of u λ is always contained in the jump set of f. Before stating this result let us recall two simple lemmas.
Lemma 2.
Let U be an open set in 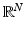 and v ∈ W 2,p (U), p ≥ 1. We have that
and v ∈ W 2,p (U), p ≥ 1. We have that
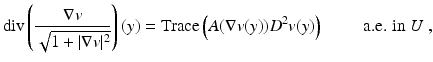 where
where 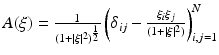 ,
, 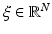 .
.
 and v ∈ W 2,p (U), p ≥ 1. We have that
and v ∈ W 2,p (U), p ≥ 1. We have that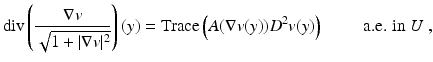
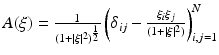 ,
, 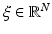 .
.The proof follows simply by taking  , integrating by parts in U, and regularizing v with a smoothing kernel.
, integrating by parts in U, and regularizing v with a smoothing kernel.
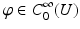 , integrating by parts in U, and regularizing v with a smoothing kernel.
, integrating by parts in U, and regularizing v with a smoothing kernel.Lemma 3.
Let U be an open set in 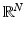 and v ∈ W 2,1 (U). Assume that u has a minimum at y 0 ∈ U and
and v ∈ W 2,1 (U). Assume that u has a minimum at y 0 ∈ U and
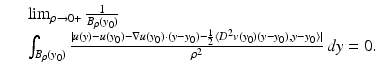
Then D 2 v(y 0 ) ≥ 0.
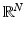 and v ∈ W 2,1 (U). Assume that u has a minimum at y 0 ∈ U and
and v ∈ W 2,1 (U). Assume that u has a minimum at y 0 ∈ U and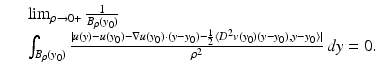
(15)
If A is a symmetric matrix and we write A ≥ 0 (respectively, A ≤ 0) we mean that A is positive (resp., negative) semidefinite.
The result follows by proving that  -a.e. for ξ in S N−1 (the unit sphere in
-a.e. for ξ in S N−1 (the unit sphere in  ) we have
) we have  .
.
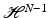 -a.e. for ξ in S N−1 (the unit sphere in
-a.e. for ξ in S N−1 (the unit sphere in 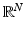 ) we have
) we have 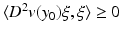 .
.Theorem 2.
Let 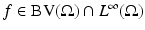 . Then, for all λ > 0,
. Then, for all λ > 0,
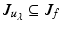
(up to a set of zero 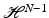 -measure).
-measure).
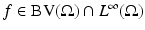 . Then, for all λ > 0,
. Then, for all λ > 0,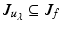
(16)
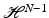 -measure).
-measure). Before giving the proof let us explain its main idea which is quite simple. Notice that, by (14), formally the Euler–Lagrange equation satisfied by ∂ E t is
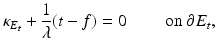 where
where 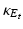 is the sum of the principal curvatures at the points of ∂ E t . Thus if
is the sum of the principal curvatures at the points of ∂ E t . Thus if 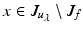 , then we may find two values t 1 < t 2 such that
, then we may find two values t 1 < t 2 such that 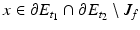 . Notice that
. Notice that 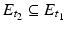 and the boundaries of both sets have a contact at x. Of the two, the smallest level set is the highest and has smaller mean curvature. This contradicts its contact at x.
and the boundaries of both sets have a contact at x. Of the two, the smallest level set is the highest and has smaller mean curvature. This contradicts its contact at x.
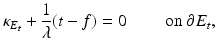
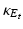 is the sum of the principal curvatures at the points of ∂ E t . Thus if
is the sum of the principal curvatures at the points of ∂ E t . Thus if 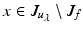 , then we may find two values t 1 < t 2 such that
, then we may find two values t 1 < t 2 such that 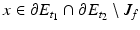 . Notice that
. Notice that 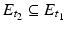 and the boundaries of both sets have a contact at x. Of the two, the smallest level set is the highest and has smaller mean curvature. This contradicts its contact at x.
and the boundaries of both sets have a contact at x. Of the two, the smallest level set is the highest and has smaller mean curvature. This contradicts its contact at x.Proof.
Let us first recall some consequences of Corollary 1. Let E t : = { u λ > t}, 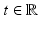 , and let
, and let 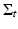 be its singular set given by Corollary 1. Since
be its singular set given by Corollary 1. Since 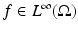 , around each point
, around each point 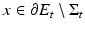 ,
, 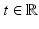 , ∂ E t is locally the graph of a function in W 2, p for all p ∈ [1, ∞) (hence C 1, α for any α ∈ (0, 1)). Moreover, if
, ∂ E t is locally the graph of a function in W 2, p for all p ∈ [1, ∞) (hence C 1, α for any α ∈ (0, 1)). Moreover, if 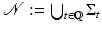 , then
, then 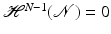 .
.
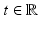 , and let
, and let 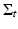 be its singular set given by Corollary 1. Since
be its singular set given by Corollary 1. Since 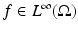 , around each point
, around each point 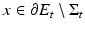 ,
, 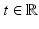 , ∂ E t is locally the graph of a function in W 2, p for all p ∈ [1, ∞) (hence C 1, α for any α ∈ (0, 1)). Moreover, if
, ∂ E t is locally the graph of a function in W 2, p for all p ∈ [1, ∞) (hence C 1, α for any α ∈ (0, 1)). Moreover, if 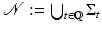 , then
, then 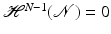 .
.Let us prove that 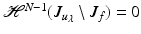 . Observe that we may write [9]
. Observe that we may write [9]
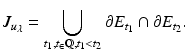 Thus it suffices to prove that for all
Thus it suffices to prove that for all  , t 1 < t 2, we have
, t 1 < t 2, we have
Let us denote by B R ′ the ball of radius R > 0 in  centered at 0. Let C R : = B R ′ × (−R, R). Let us fix
centered at 0. Let C R : = B R ′ × (−R, R). Let us fix  , t 1 < t 2. Given
, t 1 < t 2. Given  , by Corollary 1, we know that there is some R > 0 such that, after a change of coordinates that aligns the x N -axis with the normal to
, by Corollary 1, we know that there is some R > 0 such that, after a change of coordinates that aligns the x N -axis with the normal to 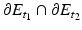 at x, we may write the set
at x, we may write the set 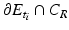 as the graph of a function v i ∈ W 2, p (B R ′ ),
as the graph of a function v i ∈ W 2, p (B R ′ ), 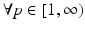 ,
, 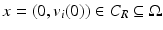 , ∇v i (0) = 0, i ∈ { 1, 2}. Without loss of generality, we assume that v i > 0 in B R ′ , and that
, ∇v i (0) = 0, i ∈ { 1, 2}. Without loss of generality, we assume that v i > 0 in B R ′ , and that 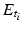 is the supergraph of v i , i = 1, 2. From t 1 < t 2 and Lemma 1, it follows
is the supergraph of v i , i = 1, 2. From t 1 < t 2 and Lemma 1, it follows 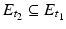 , which gives in turn v 2 ≥ v 1 in B R ′ .
, which gives in turn v 2 ≥ v 1 in B R ′ .
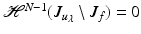 . Observe that we may write [9]
. Observe that we may write [9]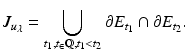
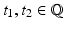 , t 1 < t 2, we have
, t 1 < t 2, we have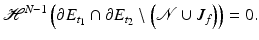
(17)
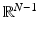 centered at 0. Let C R : = B R ′ × (−R, R). Let us fix
centered at 0. Let C R : = B R ′ × (−R, R). Let us fix 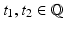 , t 1 < t 2. Given
, t 1 < t 2. Given 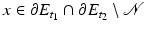 , by Corollary 1, we know that there is some R > 0 such that, after a change of coordinates that aligns the x N -axis with the normal to
, by Corollary 1, we know that there is some R > 0 such that, after a change of coordinates that aligns the x N -axis with the normal to 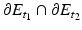 at x, we may write the set
at x, we may write the set 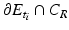 as the graph of a function v i ∈ W 2, p (B R ′ ),
as the graph of a function v i ∈ W 2, p (B R ′ ), 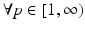 ,
, 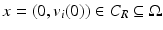 , ∇v i (0) = 0, i ∈ { 1, 2}. Without loss of generality, we assume that v i > 0 in B R ′ , and that
, ∇v i (0) = 0, i ∈ { 1, 2}. Without loss of generality, we assume that v i > 0 in B R ′ , and that 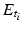 is the supergraph of v i , i = 1, 2. From t 1 < t 2 and Lemma 1, it follows
is the supergraph of v i , i = 1, 2. From t 1 < t 2 and Lemma 1, it follows 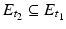 , which gives in turn v 2 ≥ v 1 in B R ′ .
, which gives in turn v 2 ≥ v 1 in B R ′ .Notice that, since 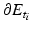 is of finite
is of finite 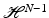 measure, we may cover
measure, we may cover 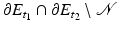 by a countable set of such cylinders. Thus, it suffices to prove that
by a countable set of such cylinders. Thus, it suffices to prove that
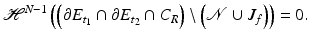
holds for any such cylinder C R as constructed in the last paragraph.
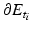 is of finite
is of finite 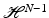 measure, we may cover
measure, we may cover 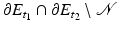 by a countable set of such cylinders. Thus, it suffices to prove that
by a countable set of such cylinders. Thus, it suffices to prove that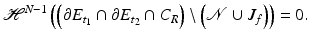
(18)
Recall that, by Theorem 3.108 in [9], 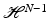 -a.e. in y ∈ B R ′ , the function f(y, ⋅ ) ∈ BV((−R, R)) and the jumps of f(y, ⋅ ) are the points z such that (y, z) ∈ J f . Recall that v i is a local minimizer of
-a.e. in y ∈ B R ′ , the function f(y, ⋅ ) ∈ BV((−R, R)) and the jumps of f(y, ⋅ ) are the points z such that (y, z) ∈ J f . Recall that v i is a local minimizer of
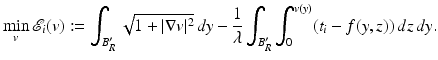 By taking a positive smooth test function ψ(y) of compact support in B R ′ , and computing
By taking a positive smooth test function ψ(y) of compact support in B R ′ , and computing 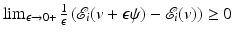 , we deduce that
, we deduce that
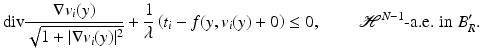
In a similar way, we have
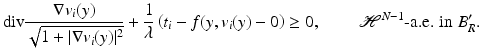
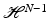 -a.e. in y ∈ B R ′ , the function f(y, ⋅ ) ∈ BV((−R, R)) and the jumps of f(y, ⋅ ) are the points z such that (y, z) ∈ J f . Recall that v i is a local minimizer of
-a.e. in y ∈ B R ′ , the function f(y, ⋅ ) ∈ BV((−R, R)) and the jumps of f(y, ⋅ ) are the points z such that (y, z) ∈ J f . Recall that v i is a local minimizer of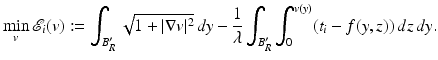
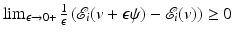 , we deduce that
, we deduce that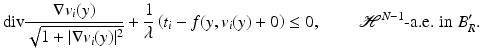
(20)
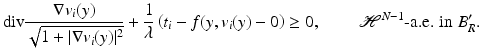
(21)
Finally we observe that since 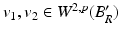 for any p ∈ [1, ∞) and v 2 ≥ v 1 in B R ′ , by Lemma 3 we have that D 2(v 1 − v 2)(y) ≤ 0
for any p ∈ [1, ∞) and v 2 ≥ v 1 in B R ′ , by Lemma 3 we have that D 2(v 1 − v 2)(y) ≤ 0 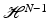 -a.e. on
-a.e. on 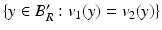 .
.
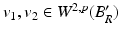 for any p ∈ [1, ∞) and v 2 ≥ v 1 in B R ′ , by Lemma 3 we have that D 2(v 1 − v 2)(y) ≤ 0
for any p ∈ [1, ∞) and v 2 ≥ v 1 in B R ′ , by Lemma 3 we have that D 2(v 1 − v 2)(y) ≤ 0 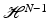 -a.e. on
-a.e. on 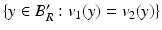 .
.Thus, if 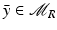 such that
such that 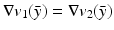 ,
, 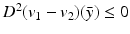 ,
, 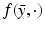 is continuous at
is continuous at 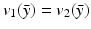 , and both Eqs. (20) and (21) hold at
, and both Eqs. (20) and (21) hold at 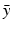 . As a consequence, using Lemma 2 and subtracting the two equations, we obtain
. As a consequence, using Lemma 2 and subtracting the two equations, we obtain
![$$\displaystyle{0 \geq \mathrm{ trace}(A(\nabla v_{1}(\bar{y}))D^{2}v_{ 1}(\bar{y})) -\mathrm{ trace}(A(\nabla v_{2}(\bar{y}))D^{2}v_{ 2}(\bar{y})) = \frac{t_{2} - t_{1}} {\lambda } > 0,}$$” src=”/wp-content/uploads/2016/04/A183156_2_En_23_Chapter_Equp.gif”></DIV></DIV></DIV>This contradiction proves (<SPAN class=InternalRef><A href=]() 19). □
19). □
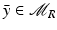 such that
such that 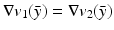 ,
, 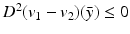 ,
, 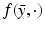 is continuous at
is continuous at 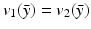 , and both Eqs. (20) and (21) hold at
, and both Eqs. (20) and (21) hold at 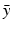 . As a consequence, using Lemma 2 and subtracting the two equations, we obtain
. As a consequence, using Lemma 2 and subtracting the two equations, we obtainHölder Regularity Results
Let us review the local regularity result proved in [23]: if the datum f is locally Hölder continuous with exponent β ∈ [0, 1] in some region  , then a local minimizer u of (13) is also locally Hölder continuous in
, then a local minimizer u of (13) is also locally Hölder continuous in 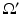 with the same exponent.
with the same exponent.
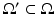 , then a local minimizer u of (13) is also locally Hölder continuous in
, then a local minimizer u of (13) is also locally Hölder continuous in 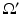 with the same exponent.
with the same exponent.Recall that a function 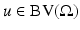 is a local minimizer of (13) if for any
is a local minimizer of (13) if for any 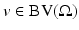 such that u − v has support in a compact subset
such that u − v has support in a compact subset 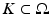 , we have
, we have
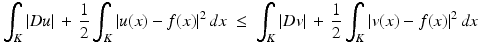
It follows that u satisfies the equation [18]
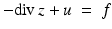
with 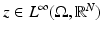 with
with 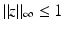 , and z ⋅ Du = | Du | [10].
, and z ⋅ Du = | Du | [10].
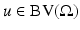 is a local minimizer of (13) if for any
is a local minimizer of (13) if for any 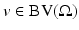 such that u − v has support in a compact subset
such that u − v has support in a compact subset 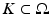 , we have
, we have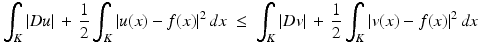
(22)
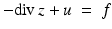
(23)
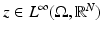 with
with 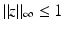 , and z ⋅ Du = | Du | [10].
, and z ⋅ Du = | Du | [10].As in section “The Discontinuities of Solutions of the TV Denoising Problem” [20], the analysis of the regularity of the local minimizers of u is based on the following observation: for any 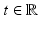 , the level sets {u > t} (resp., {u ≥ t}) are solutions (the minimal and maximal, indeed) of the prescribed curvature problem (14) which is defined in the class of finite-perimeter sets and hence up to a Lebesgue-negligible set. The local regularity of u can be described in terms of the distance of any two of its level sets. This is the main idea in [20] which can be refined to obtain the Hölder regularity of solutions of (14). As we argued in section “The Discontinuities of Solutions of the TV Denoising Problem,” outside the jump discontinuities of f (modulo an
, the level sets {u > t} (resp., {u ≥ t}) are solutions (the minimal and maximal, indeed) of the prescribed curvature problem (14) which is defined in the class of finite-perimeter sets and hence up to a Lebesgue-negligible set. The local regularity of u can be described in terms of the distance of any two of its level sets. This is the main idea in [20] which can be refined to obtain the Hölder regularity of solutions of (14). As we argued in section “The Discontinuities of Solutions of the TV Denoising Problem,” outside the jump discontinuities of f (modulo an 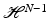 -null set), any two level sets at different heights cannot touch and hence the function u is continuous there. To be able to assert a Hölder type regularity property for u one needs to prove a local estimate of the distance of the boundaries of two level sets. This can be done here under the assumption of local Hölder regularity for f [23].
-null set), any two level sets at different heights cannot touch and hence the function u is continuous there. To be able to assert a Hölder type regularity property for u one needs to prove a local estimate of the distance of the boundaries of two level sets. This can be done here under the assumption of local Hölder regularity for f [23].
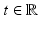 , the level sets {u > t} (resp., {u ≥ t}) are solutions (the minimal and maximal, indeed) of the prescribed curvature problem (14) which is defined in the class of finite-perimeter sets and hence up to a Lebesgue-negligible set. The local regularity of u can be described in terms of the distance of any two of its level sets. This is the main idea in [20] which can be refined to obtain the Hölder regularity of solutions of (14). As we argued in section “The Discontinuities of Solutions of the TV Denoising Problem,” outside the jump discontinuities of f (modulo an
, the level sets {u > t} (resp., {u ≥ t}) are solutions (the minimal and maximal, indeed) of the prescribed curvature problem (14) which is defined in the class of finite-perimeter sets and hence up to a Lebesgue-negligible set. The local regularity of u can be described in terms of the distance of any two of its level sets. This is the main idea in [20] which can be refined to obtain the Hölder regularity of solutions of (14). As we argued in section “The Discontinuities of Solutions of the TV Denoising Problem,” outside the jump discontinuities of f (modulo an 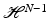 -null set), any two level sets at different heights cannot touch and hence the function u is continuous there. To be able to assert a Hölder type regularity property for u one needs to prove a local estimate of the distance of the boundaries of two level sets. This can be done here under the assumption of local Hölder regularity for f [23].
-null set), any two level sets at different heights cannot touch and hence the function u is continuous there. To be able to assert a Hölder type regularity property for u one needs to prove a local estimate of the distance of the boundaries of two level sets. This can be done here under the assumption of local Hölder regularity for f [23].Theorem 3.
Let N ≤ 7 and let u be a solution of (23) . Assume that f is in C 0,β locally in some open set 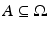 , for some β ∈ [0,1]. Then u is also C 0,β locally in A.
, for some β ∈ [0,1]. Then u is also C 0,β locally in A.
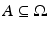 , for some β ∈ [0,1]. Then u is also C 0,β locally in A.
, for some β ∈ [0,1]. Then u is also C 0,β locally in A. The Lipschitz case corresponds to β = 1.
One can also state a global regularity result for solutions of the Neumann problem when 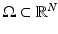 is a convex domain. Let
is a convex domain. Let 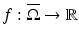 be a uniformly continuous function, with modulus of continuity
be a uniformly continuous function, with modulus of continuity 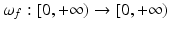 , that is, | f(x) − f(y) | ≤ ω f ( | x − y | ) for all
, that is, | f(x) − f(y) | ≤ ω f ( | x − y | ) for all 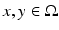 . We consider the solution u of (23) with homogeneous Neumann boundary condition, that is, such that (22) for any compact set
. We consider the solution u of (23) with homogeneous Neumann boundary condition, that is, such that (22) for any compact set 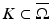 and any
and any 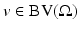 such that v = u out of K. This solution is unique, as can be shown adapting the proof of [18, Cor. C.2.] (see also [10] for the required adaptations to deal with the boundary condition), which deals with the case
such that v = u out of K. This solution is unique, as can be shown adapting the proof of [18, Cor. C.2.] (see also [10] for the required adaptations to deal with the boundary condition), which deals with the case 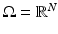 .
.
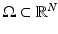 is a convex domain. Let
is a convex domain. Let 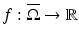 be a uniformly continuous function, with modulus of continuity
be a uniformly continuous function, with modulus of continuity 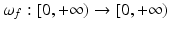 , that is, | f(x) − f(y) | ≤ ω f ( | x − y | ) for all
, that is, | f(x) − f(y) | ≤ ω f ( | x − y | ) for all 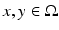 . We consider the solution u of (23) with homogeneous Neumann boundary condition, that is, such that (22) for any compact set
. We consider the solution u of (23) with homogeneous Neumann boundary condition, that is, such that (22) for any compact set 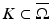 and any
and any 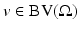 such that v = u out of K. This solution is unique, as can be shown adapting the proof of [18, Cor. C.2.] (see also [10] for the required adaptations to deal with the boundary condition), which deals with the case
such that v = u out of K. This solution is unique, as can be shown adapting the proof of [18, Cor. C.2.] (see also [10] for the required adaptations to deal with the boundary condition), which deals with the case 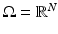 .
.Then, the following result holds true [23]:
Theorem 4.
Assume N ≤ 7. Then, the function u is uniformly continuous in 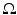 , with modulus ω u ≤ω f.
, with modulus ω u ≤ω f.
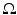 , with modulus ω u ≤ω f.
, with modulus ω u ≤ω f.Again, it is quite likely here that the assumption N ≤ 7 is not necessary for this result.
4 Some Explicit Solutions
Recall that a convex body in 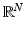 is a compact convex subset of
is a compact convex subset of  . We say that a convex body is nontrivial if it has nonempty interior.
. We say that a convex body is nontrivial if it has nonempty interior.
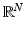 is a compact convex subset of
is a compact convex subset of  . We say that a convex body is nontrivial if it has nonempty interior.
. We say that a convex body is nontrivial if it has nonempty interior.We want to exhibit the explicit solution of (13) when f = χ C and C is a nontrivial convex body in 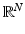 . This will show that the preservation of a jump discontinuity depends on the curvature of
. This will show that the preservation of a jump discontinuity depends on the curvature of 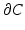 at the given point, the size of the jump, and the regularization parameter λ.
at the given point, the size of the jump, and the regularization parameter λ.
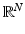 . This will show that the preservation of a jump discontinuity depends on the curvature of
. This will show that the preservation of a jump discontinuity depends on the curvature of 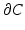 at the given point, the size of the jump, and the regularization parameter λ.
at the given point, the size of the jump, and the regularization parameter λ.Let u λ, C be the unique solution of the problem:
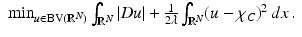
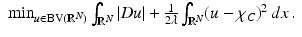
(24)
The following result was proved in [5].
Proposition 2.
We have that 0 ≤ u λ,C ≤ 1, u λ,C = 0 in 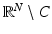 , and u λ,C is concave in {u λ,C > 0}.
, and u λ,C is concave in {u λ,C > 0}.
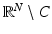 , and u λ,C is concave in {u λ,C > 0}.
, and u λ,C is concave in {u λ,C > 0}. The proof of 0 ≤ u λ, C ≤ 1 follows from a weak version of the maximum principle [5]. Thanks to the convexity of C, by comparison with the characteristic function of hyperplanes, one can show that u λ, C = 0 out of C [5]. To prove that u λ, C is concave in {u λ, C > 0} one considers first the case where C is of class C 1, 1 and λ > 0 is small enough. Then one proves that u λ, C is concave by approximating u λ, C by the solution u ε of
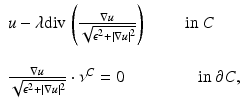
as ε → 0+, using Korevaar’s concavity Theorem [46]. Then one considers the case where C is of class C 1, 1 and we take any λ > 0. In this case, the concavity of u λ, C in {u λ, C > 0} is derived after proving Theorems 5 and 6 below. The final step proceeds by approximating a general convex body C by convex bodies of class C 1, 1 [4].
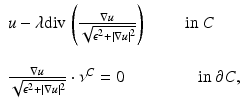
(25)
Moreover, since u λ, C = 0 out of C, the upper level set {u λ, C > s} ⊆ C for any s ∈ (0, 1]. Then, as in Proposition 1, one can prove that for any s ∈ (0, 1] the level set {u λ, C > s} is a solution of
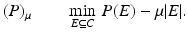
for the value of μ = λ −1(1 − s). When taking λ ∈ (0, +∞) and s ∈ (0, 1] we are able to cover the whole range of μ ∈ [0, ∞) [5]. By Lemma 1 we know that if μ < μ ′ and 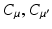 are minimizers of (P) μ
are minimizers of (P) μ




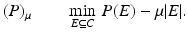
(26)
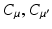 are minimizers of (P) μ
are minimizers of (P) μ
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree