Device
References
SPECT
AXIS
DST Xli
Millenium VG
Symbia
(Staelens et al. 2003)
(Autret et al. 2005)
PET
ECAT Exact HR+
HRRT
Advance Discovery
Allegro/Gemini
Hi-Rez
Biograph
(Jan et al. 2005a)
(Bataille et al. 2004)
(Schmidtlein et al. 2006)
(Lamare et al. 2006)
(Michel et al. 2006)
(Gonias et al. 2007)
Animal imaging devices
μPET P4
Focus 220
Mosaic
ClearPET
OPET
Inveon
(Jan et al. 2003)
(Jan et al. 2005b)
(Merheb et al. 2006)
(Rey et al. 2007)
(Rannou et al. 2004)
(Dartial et al. 2009)
3 Monte Carlo Methods for Nuclear Medicine Imaging
The relevance of Monte Carlo codes in nuclear medicine imaging is multiple:
Detector modelling can be carried out in order to evaluate/optimise in silico the behaviour of a prototype. In addition, detector modelling is a component of imaging modelling, since it usually results in determining the imaging system response.
Imaging modelling can serve various purposes:
Study/optimisation of reconstruction/correction approaches.
Study of the imaging process.
In addition, Monte Carlo can be used to generate clinical images and thus implement image databases.
3.1 Detector Modelling
Modelling a SPECT or PET imaging device has become quite a common task with recent/specific Monte Carlo codes such as Gate. It is interesting to note that one of the first attempts to model a gamma camera by the Nantes group (Autret et al. 2005) required a significant part of a PhD project, whereas more recent camera modelling just required a Master project (Carlier et al. 2008).
Modelling a SPECT device requires first a good knowledge of the dimension and composition of the detector head. However, even with modern MC codes, it is not possible to fully model a detector head, including for example the photomultipliers: a certain degree of simplification has to be accepted. This is why most studies modelling a SPECT head consider the volume behind the detector crystal as a homogeneous compartment made of Perspex or equivalent, with variable thickness and density.
Since SPECT imaging is mostly conditioned by the characteristics of the collimator, the modelling of the collimator and how impacting photons are processed represent a major feature of SPECT modelling. First of all, about one out of 100,000 incident photons are transmitted through the collimator and impact the crystal. This explains why the explicit modelling of photons within the collimator always requires a very significant amount of computing time.
In some situations (i.e. Tc-99m imaging with low-energy collimators), it is reasonable to assume that photons impacting a collimator lead septum are likely to be stopped. This is why some codes like SimSET consider the transmission of photons through the collimator as a geometrical (solid angle) process only. However, for high energy isotopes such as I-131, septal penetration cannot be neglected, and the processes occurring in the collimator have to be modelled. Some codes like Gate allow for the definition of “realistic” collimators, including “cast” and “foil” collimators (Staelens et al. 2003). However, the time penalty associated with the explicit modelling of processes within the collimator has led some authors to present alternatives where the response of the collimator is tabulated in pre-calculated tables (Song et al. 2005). This elegant approach can accelerate the simulation by a factor of 100 or more (Descourt et al. 2010).
3.2 Quantitative Imaging
Satisfying image quantification is only possible if all effects that degrade the quantitative content of the image have been corrected for. Monte Carlo simulations can help to model interactions occurring in the patient and in the detector system. This is helpful to develop and test correction techniques, and to help to define detector geometries better suited to quantitative imaging. As a consequence there are a growing number of articles (Buvat and Castiglioni 2002; Zaidi 1999, 2000) and textbooks (Ljungberg et al. 1998; Zaidi and Sgouros 2003; Zaidi 2006) being published in the field of nuclear medicine that involve Monte Carlo techniques particularly with respect to quantitative imaging (Holstensson et al. 2010).
As an example a Monte Carlo simulation of the influence of septal penetration and scatter of I-131 photons on a high-energy collimator of a gamma camera is shown in Fig. 1 (top left: resulting image, top right: scatter only, bottom left: septal penetration, bottom right: geometric photons). The numbers in the upper right corner denote the percentage of photons (Autret et al. 2005). In the case of I-131, even for a very simple situation of a point source in air, only 47 % of detected photons counted by a gamma camera are in fact geometric photons: the rest comes either from septal penetration or scatter. This highlights the importance of the collimator in high-energy imaging, as initially reported by Dewaraja et al. (2000).


Fig. 1
Monte Carlo simulation of the influence of septal penetration and scatter of I-131 photons on a high-energy collimator of a gamma camera (top left resulting image, top right scatter only, bottom left septal penetration, bottom right geometric photons)
4 Monte Carlo Methods for Nuclear Medicine Radiation Transport Calculations
Dosimetric estimates in Nuclear Medicine require both quantitative imaging and a calculation of the absorbed dose rate per unit activity (the so-called S-factor). The S-factor describes, for a given geometry and isotope, the energy imparted by ionising radiation to a given voxel, tissue or organ. Historically, Monte Carlo simulations were first used for S-factor calculations and are the obvious field to use Monte Carlo methods in nuclear medicine:
An analytical description of radiation transport is only feasible in a restricted number of cases—basically for very simple geometries and uniform propagation media. The pioneer work of Berger (Berger 1963) was first used for Monte Carlo determination of dose point kernels (DPKs) that were previously determined by numerical solving of the radiation transport equations (Berger 1971, 1973). A further step was reached with the modelling of dose deposition in heterogeneous phantoms (Snyder et al. 1969), which eventually led to the publication of the MIRD S-factor tables for an adult reference man (Snyder et al. 1975). Cristy and Eckerman (1987) published S-factors for 6 anthropomorphic phantoms representing the newborn, 1, 5, 10 and 15-years-old child (at the time considered as equivalent to the reference women) and the reference adult male. These were later integrated in the MIRDOSE software (version 2) (Stabin 1996). At the time, due to calculation time constraint, a large degree of uncertainty had to be accepted. Phantom geometry was built using a combination of simple, elementary shapes defined by equations, thus leading to “mathematical phantoms”. Since then, the availability of an ever-increasing computing power allowed for the generation of more sophisticated mathematical or even voxel-based phantoms, including ethnic phantoms, or male or female phantoms of varying size and weight (Clairand et al. 2000; Saito et al. 2001; Xu et al. 2000; Blaickner and Kindl 2008; Lee et al. 2007; Ferrari and Gualdrini 2007; Yamauchi et al. 2005; Stabin and Yoriyaz 2002).
However sophisticated, a dosimetric approach based on mathematical phantom remains within the domain of “model dosimetry”, i.e. in principle not applicable to “real” patients. Monte Carlo-based patient-specific dosimetry requires using patient-specific data to define both geometry and pharmacokinetics. This somehow looks easy with the advent of hybrid machines that provide for both anatomy (CT) and activity (SPECT or PET). However, patient-specific absorbed dose calculation through Monte Carlo simulation is difficult to achieve—at least when the whole patient body (and internal organs) is considered. An example given by Xu (2005) emphasises this point: the reference man, when segmented with a (quite good) sampling of 0.3 × 0.3 × 1 mm leads to a 4 GB data set, which exceeds the limits of most 32 bytes workstations (by contrast, defining a stylised patient—i.e. a mathematical phantom—only leads to an input file of some kilobytes). It is also generally felt that dealing with digital phantoms (i.e. the closest data set to a ‘real’ patient image) dramatically increases the calculation time required performing Monte Carlo simulations (Caon 2004). However, some examples have recently been published that seem to indicate that patient-specific absorbed dose calculations with Monte Carlo techniques is feasible and may become more spread in the near future (Caon 2004; Chiavassa et al. 2006; Descalle et al. 2003; Peter et al. 2000; Xu 2005; Yoriyaz et al. 2000). Comparison of reference models and patient-specific anatomy has also investigated the relevance of adjusting S-factors by the organ mass ratios (Divoli et al. 2009).
5 Monte Carlo Methods Applied to Nuclear Medicine Dosimetry
Several software packages for nuclear medicine dosimetry have been developed to combine quantitative imaging and the S-value methodology based on Monte Carlo Methods.
MABDOSE (University of Colorado) implements fixed geometry and allows the user to place spherically shaped tumours within the simplified anatomic model originally described by the MIRD Committee. To do this, an on-the-fly Monte Carlo simulation was incorporated into the code (Johnson et al. 1999a, b). This method could accommodate tumour dosimetry within the idealised geometry defined by the MIRD Committee.
The consequence of using these programs is that in general it is not possible to include or recalculate patient-specific S-factors as they are based on fixed geometries. How much this fact contributes to the uncertainty in patient-specific assessments of the absorbed dose is highly dependent upon the disease and the radiopharmaceutical used. In some cases the patient specificity does not influence the result greatly, whereas in other cases a complete over- or underestimation of the dose is possible.
A more comprehensive approach is to calculate the absorbed dose distribution throughout the tumour and generate dose-volume histograms (Sgouros et al. 1990). This can be achieved by registering sequential tomographic data, so that each voxel within the VOI occupies the same coordinate throughout the series of scans. The mean absorbed dose in each voxel can then be calculated independently for each coordinate. For this technique voxel S-values are required. MIRD pamphlet 17 (Bolch et al. 1999) gives point-kernel and Monte Carlo-based S-values for a range of radionuclides for voxels with edges of 0.1, 3 and 6 mm. Image registration is becoming a more routinely used tool in medicine, due largely to an increasing interest in the incorporation of functional and MR data with CT for external beam radiotherapy planning and by the advent of dual modality scanners.
A second group of dosimetry software codes completely relies upon 3D imaging and voxel-based dosimetry. Many researchers have pursued and contributed to 3D imaging-based patient-specific dosimetry (Furhang et al. 1996; Chiavassa et al. 2006; Dewaraja et al. 2005; Divoli et al. 2009; Lehmann et al. 2005; Sgouros et al. 2008; Yoriyaz et al. 2001).
In principle, the codes take the distribution of a radiopharmaceutical for a given patient (from SPECT or PET) and combine it with anatomic information (from CT or MRI) to yield absorbed dose estimates that are specific to a particular patient’s biodistribution and anatomy (Sgouros 2005). In addition, some of the codes introduce the concept of dose-volume histograms for internally administered radionuclides. Dose calculations can be done applying either Monte Carlo or point-kernel-based calculations.
More recently, the computer code 3D-ID has been used in thyroid cancer patients with I-124 PET data and CT (Sgouros et al. 2004). DOSIMG software, developed by the Lund group, has been used with mathematical anthropomorphic phantoms to examine the impact of different quantitative SPECT algorithms on Monte Carlo-derived absorbed dose calculations. Mathematical phantom–derived CT and SPECT images were generated, and dose calculations derived from these were compared with “true” dose results derived from the actual mathematical phantom data (Sjogreen et al. 2005). The SPECT quantification methodologies derived from this work were subsequently applied to In-111/Y-90 dosimetry (Sjogreen et al. 2005).
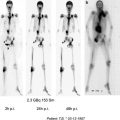
An example of patient-specific dosimetry for hepatocarcinoma treatment with 131I-Lipiodol™ carried out using Oedipe is shown in Fig. 2 (Chiavassa et al. 2005). Quantitative SPECT imaging at days 0, 3 and 7 were used to derive voxel-based cumulated activity (2.21 × 2.21 × 4.42 mm3 voxels). Monte Carlo absorbed dose calculations were performed with Oedipe for a volume of 194 × 140 × 90 voxels. Computation performed on an average desktop computer took 4 days in order to get a statistical uncertainty below 10 % for all voxels in the tumour volume. The isodoses are superimposed on CT slices.
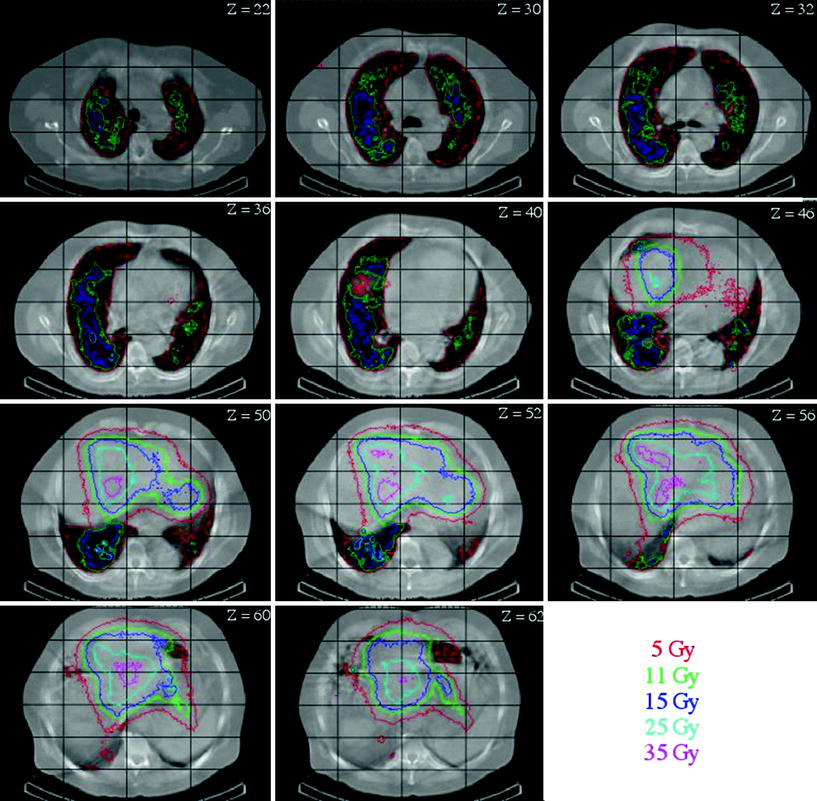

Fig. 2
Monte Carlo-based patient-specific dosimetry for hepatocarcinoma treatment with 131I-Lipiodol™ (Chiavassa et al. 2005)
6 Monte Carlo Limits
One major limit of Monte Carlo methods is linked to the statistics required to accurately simulate a given experimental setting: The number of simulated particles has to be very high, and therefore implies heavy computing power.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree