Chapter 4

Equilibrium–Saturation

Objectives

At the completion of this chapter, the student should be able to do the following:

• Define net magnetization and its relationship to equilibrium, partial saturation, and saturation.

• Distinguish between a hard and a soft radiofrequency (RF) pulse.

• Identify the primary magnetic resonance (MR) signal.

• Draw a two-line RF pulse sequence and label all of its components.

Key Terms

Free induction decay

Longitudinal relaxation

Saturated

Transverse relaxation

Chapter 3 concluded with an explanation of net magnetization, vector diagrams, and reference frames. Some of this discussion is repeated to properly develop the origin of the radio signal that results in the magnetic resonance image. Furthermore, the discussion involves the rotating frame of reference, not the stationary frame.

It is first necessary to consider more closely the way the magnetic resonance imaging (MRI) signal arises. The two basic properties of a nucleus that are important to this signal are the nuclear magnetic moment and spin.

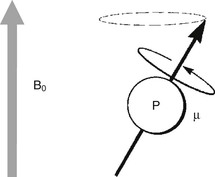
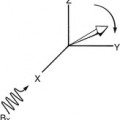
When a sample is placed in an external magnetic field, as indicated by B₀ in Figure 4-1, the nuclei attempt to align with this field. The nuclei act like tiny bar magnets, each seeking to orient itself with the external magnetic field.

In MRI, the frequency of precession depends on the type of nucleus and the intensity of the external magnetic field.

FIGURE 4-1 In the presence of an external magnetic field, protons align with the field and precess at the Larmor frequency.

The spin of the nucleus adds a complicating factor. Instead of each nucleus acting like a simple bar magnet, it behaves like a spinning bar magnet. Rather than just aligning with the external field, the nucleus precesses around the axis of the external magnetic field, as described by the Larmor equation.

Net Magnetization

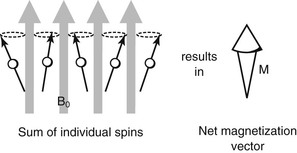
A patient placed in an MRI system consists of a multitude of proton spins. Many of these protons attempt to align with the external field and precess at the Larmor frequency (Figure 4-2). Although all the protons shown are oriented in an upward direction, the exact direction to which they point at any instant is slightly different because they are at random positions in their precession. The net result is that the individual magnetizations sum to a net magnetization (M) parallel to the direction of the external magnetic field.

Equilibrium

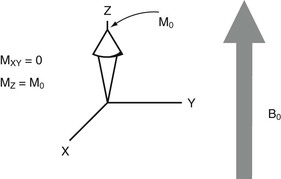
In the preceding situation, the net magnetization does not precess but is a vector of constant magnitude pointed in the direction of the external magnetic field, which is the Z direction. Because they are randomly oriented, the horizontal or X and Y components of all the individual nuclear spins are out of phase, and therefore there is no net magnetization in the XY plane.

This state of the net magnetization is called equilibrium. The proton spins are said to be at equilibrium with the external magnetic field.

The magnitude of the net magnetization at equilibrium along the Z-axis, symbolized as M₀, is determined by several physical factors. The more protons available for alignment, the larger M₀ will be.

The number of nuclei available that do align is determined by the intensity of the external magnetic field. Finally, a large gyromagnetic ratio results in a large M₀. Therefore N (the number of nuclei available), B₀, and γ contribute to M₀.

The larger the M₀, the stronger the MR signal will be.

Unfortunately, the component of M along the Z-axis cannot be measured directly. It is much too weak compared with B₀ to be detected. Only components of the net magnetization vector in the XY plane, that is, M_XY, can be detected by the MRI receiving coil.

There is no magnetization in the XY plane, M_XY. The nuclear spins are all randomly oriented in these directions; therefore it makes no sense to refer to stationary magnetization along either the X- or Y-axis. At equilibrium, no signal is received from the patient because the net magnetization vector, M, points only in the Z direction, M_Z, and has no component in the XY plane, M_XY (Figure 4-3).

FIGURE 4-3 At equilibrium, there is no XY component to net magnetization, and the Z component is at its maximum value, M₀.

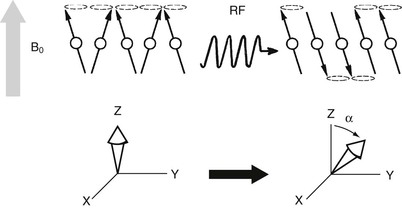
For a signal to be received from a patient, the magnetization vector must be rotated from the Z-axis so that it has some nonzero component in the XY plane. This rotation follows a pulse of radiofrequency (RF) tuned to the nuclei’s Larmor frequency. If the RF is not at this frequency, the nuclei do not absorb energy, and the net magnetization is not rotated.