Fig. 1.1
(Left) Generation and propagation of sound waves. (Centre) Shortening of sound waves caused by an approaching acoustic source. (Right) Prolongation of sound waves when the acoustic source is moving away
The middle sequence of Fig. 1.1 shows a sound generator operating at the same frequency but moving to the right at a uniform speed of 100 m/s. At the beginning of the sequence, the sound generator is on the left and produces the sound pressure zone designated ‘1’. After 1 ms, this part of the sound wave is propagated 34 cm to the right due to the speed determined by the medium. However, the sound generator has also moved by 10 cm and is now already starting to emit the next pressure wave. In comparison to the stationary sound source, this second sound pressure zone has been displaced by 10 cm to the right so the spatial distance between the two pressure zones which have been produced one after the other (i.e. the wavelength) is of course shortened.
The consequence of this reduced distance is that the pressure maxima arrive at the receiver with shorter time intervals so the receiver receives more pressure zones per second than would have been the case had the sound source remained stationary. The perceived frequency is therefore higher than the frequency actually produced.
In the example described here, the sound frequency received would be 1,416 Hz instead of 1,000 Hz which was the frequency at which the sound was generated. As Doppler correctly postulated, the displacement speed of the sound source is proportional to the change in frequency.
If, on the other hand, the sound source moves away from a receiver, the distance between two sound pressure zones will increase (Fig. 1.1 right). In this example also, the sound pressure zone designated ‘1’ is emitted first and has moved about 34 cm to the right 1 ms later, due to the speed of sound in air. At the same time, the sound source has moved around 10 cm to the left and started to emit the next pressure zone from this point. The distance of 34 cm between the two pressure waves has therefore lengthened to 44 cm. A receiver would therefore receive the pressure waves with longer time intervals and would therefore register a lower frequency of just 773 Hz.
Changing the location of a sound source, however, is not the only way a frequency shift may be produced – a corresponding effect is also experienced by moving the receiver.
This phenomenon is illustrated in Fig. 1.2.


Fig. 1.2
Increase of observed frequency when the receiver is moving towards
The receiver in the figure moves at a speed of 100 m/s towards the approaching sound waves. The top of the figure shows that the pressure maximum designated ‘1’ arrives at the observer. The high pressure zone designated ‘2’ follows at a distance of 34 cm (in accordance with a sonic frequency of 1,000 Hz) and would normally reach the observer 1 ms later. Since the latter has moved closer to the sound generator by around 10 cm, the sound wave ‘2’ arrives correspondingly earlier – i.e. after less than a millisecond. The shortening of this interval corresponds to an increase in the perceived frequency from 1,000 to 1,294 Hz.
On the other hand, if the observer moves away from the transmitter, the number of sound waves detected per second decreases. This is clearly shown in Fig. 1.3. At the top of the figure, the observer hurrying away receives the sound wave designated ‘1’ at a frequency of 1,000 Hz. The wave designated ‘2’ generated after a millisecond has to travel a longer distance than sound wave ‘1’, since the observer has now moved 10 cm further away from the sound source. In this case, the interval between two reception cycles thus increased corresponds to a reduction in frequency from 1,000 to 706 Hz.


Fig. 1.3
Decrease of observed frequency when the receiver is moving away
If the departure velocity were to increase to the speed of sound, the observer would find himself moving forwards with the sound wave inside a constant pressure zone. In this extreme case, periodic pressure changes would cease to arrive at the receiver and the frequency detected would be zero.
1.1.1 Summary
Transmitter approaches receiver = increase in perceived frequency
Transmitter moves away from receiver = decrease in perceived frequency
Receiver approaches transmitter = increase in perceived frequency
Receiver moves away from transmitter = decrease in perceived frequency
Since the situation is different in each case, Christian Doppler derived a different equation to calculate the frequency shift depending on whether the sound source or the observer is moving. However, if the speed of the object is small in relation to the speed of sound, the same simplified calculation principles can be applied to both cases. Thus, the frequency shift has one proportionality ratio both for the original frequency produced by the sound generator and for the speed of the observer or the sound source. On the other hand, the frequency shift is inversely proportional to the speed of sound in the medium. The simplified equation is therefore:


The Doppler effect is certainly experienced in everyday life. For example, an observer will notice a change in pitch of the sound coming from a fast car as it passes the point of observation on a fast road. As the car approaches, the observer hears a sound which is higher pitched than the sound of the engine. Once the vehicle has reached the hearer and is moving away, the sound waves are ‘stretched’ and the observer hears the sound at a lower pitch.
The frequency also changes when the distance between the sound source and sound receiver does not change but the sound is deflected via a moving reflector (Fig. 1.4). Since the first Doppler shift has already taken place on arrival at the reflector and the second Doppler shift takes place when it is emitted at a frequency which has already changed, the frequency change is doubled.


Fig. 1.4
(a, b) Change of the observed frequency when the reflector is moving away or towards
In this case, the Doppler equation must be modified as follows:


If the original frequency is known and the reflected frequency is measured, the speed of the reflector can also be measured by rearranging the equation. This principle is used in research, medicine and industry as well as the police force, military applications and by aerospace authorities to determine the approach speed of vehicles, aircraft or rockets. In these cases, the object being checked is not subjected to sound waves but high-intensity long-range electromagnetic waves.
Different methods are available for Doppler sonographic flow measurements in medicine which will be dealt with in more detail in the following – the continuous wave Doppler, the pulsed wave Doppler and the different colour-coded Doppler techniques.
1.2 Continuous Wave Doppler Ultrasound Technique
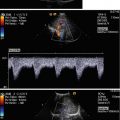
The principle of frequency shifts caused by a moving reflector described above is used to measure blood flow velocity (Satomura 1959; Strandness et al. 1967).
Ultrasound is continuously radiated into the body at a frequency between 2 and 10 MHz from a quartz crystal (Fig. 1.5). Minute components of the energy are reflected back by the tissue, vessel walls and even the surfaces of the corpuscular blood components and picked up by a second crystal. The detected ultrasound is fed to a so-called mixer where it is compared with the transmission frequency. Since there is no difference between the frequencies of the sound reflected back from the static reflecting surfaces to the frequency of the transmitted sound, the mixer will not detect any difference between them.


Fig. 1.5
Functional principle of a simple CW-Doppler without display
The moving blood cells, however, reflect back the radiated sound at a different frequency according to the Doppler principle. The greater the rate of flow, the greater the difference between the frequency of the reflected sound and the frequency of the radiated sound. With a transmission frequency of 5 MHz and a velocity of 10 cm/s, the ultrasound frequency shifts from 5,00,000 to 5,00,044 MHz. To determine the difference, the transmitted and received frequencies are superimposed so that they alternate between coincidence and noncoincidence as a result of the slight difference in wavelengths. At the same time, the amplitude is always increased by addition when both signals are exactly in phase, i.e. have the same polarity. On the other hand, if the ultrasound frequency has a positive amplitude while the other signal is negative, the net result is extinction. This produces a new frequency which corresponds exactly to the difference between the transmitted ultrasound frequency and the received ultrasound frequency. In the example here, the difference is 440 Hz, which can be heard as a howl or a hiss in the loudspeaker.
The faster the blood velocity, the greater the difference between the transmitted frequency and the received frequency and the greater the perceived difference or Doppler frequency
Since blood flows at an almost uniform rate in the veins, the noise coming from the device during a venal examination is an almost constant howl. On the other hand, the flow pulsation in the arteries causes the sound pitch to swell and subside as the Doppler frequency changes with the cardiac cycle.
Although this simplest of all Doppler devices only provides acoustic information about flow behaviours, it can be used for numerous applications in angiological diagnostics (Marshall 1984; Fischer and Wuppermann 1985; Mühlen 1989).
Since the acoustic signal from this device corresponds merely to the difference between the transmitted and received frequency, it is possible to draw conclusions on the flow velocity only – not on the flow direction. Both a blood flow towards the probe and a blood flow away from it but of identical flow velocity will produce an identical frequency shift. This technique is therefore called ‘non–directional’.
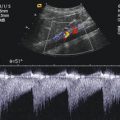
The Doppler systems which indicate the direction of flow have a wider range of applications. The signal processing system of these devices is able to detect the direction of flow in relation to the probe and display it as a velocity curve on the screen or printer (Fig. 1.6). Usually, these directional Dopplers are polarised so that flows towards the probe are displayed above and flows away from the probe are displayed below the zero line on the screen. However, this arrangement can be inverted on every commercially available device. The size of the deflection, i.e. the amplitude of the curve, reflects the flow velocity under examination.


Fig. 1.6
Print out of a Doppler curve by application of a zero crosser signal processing
Simple devices use a so-called zero crosser to convert the Doppler frequency into a proportional deflection. Here, the frequency of the Doppler signal is simply ‘counted out’ and converted into an analogue deflection (MacLeod 1967).
These devices therefore do not take into account the fact that the corpuscular blood components move at very different rates over the cross section of the vessel. Since the zero crosser is not able to record several speeds simultaneously, only the predominant speed (i.e. the speed at which the overwhelming majority of particles are moving within the observation time) appears on the screen. All other speeds are disregarded (Lunt 1975; Evans et al. 1989).
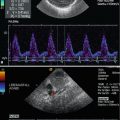
1.3 Spectral Analysis
In contrast to the zero-crossing technique, spectral analysis shows all the speeds over the cross section of the vessel (Maulik 2005). In addition to this, the frequencies or velocities on the screen are correct, so it is possible to make quantitative statements by including other measurement parameters (Warnking and Teague 1981). In principle, the velocity spectrum displayed on the screen or printer corresponds to the conventional Doppler curves with a vertical speed axis and horizontal time axis.
Figure 1.7 shows how it operates schematically. In order to show all the speeds simultaneously, the particle speeds detected are displayed on the vertical axis in the form of dots one on top of the other. Each dot therefore corresponds to a certain frequency or speed. Each speed causes its own Doppler shift so the receiving crystal detects a variety of different ultrasonic frequencies. However, since this receiving crystal cannot oscillate at all the frequencies simultaneously, they are superimposed additively to produce a new, quite complex curve shape. Inside the spectrum analyser, this frequency mix is compared with the original transmitter frequency to produce numerous different Doppler or difference frequencies. Thus, the slow velocity at the wall yields a Doppler frequency of a few Hz, while the highest speed which is often in the centre of the vessel can produce a frequency shift of up to 10 kHz or more, for example.


Fig. 1.7
Acquisition and display of a Doppler frequency spectrum
These Doppler frequencies are displayed on a vertical frequency axis on a screen in the form of pixels. Each dot therefore represents a certain frequency or speed. The intensity of each dot represents the occurrence of the corresponding speed. Thus, dots which are particularly intense indicate that there are a lot of blood cells moving at this speed.
The frequency analysis and the structure of the corresponding vertical dot line are completed after a few milliseconds. A new measurement cycle then starts immediately where the frequencies which are now determined are displayed to the right of the previous line. Thus, the picture develops line-by-line in quick succession as the speed curve is displayed to the observer and scrolls across the screen in real time.
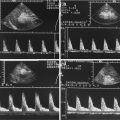
Under normal conditions, the blood flow is predominantly laminar, i.e. the corpuscular blood components flow in a straight or – as we now know – in a helical (Kilner et al. 1993) way on parallel paths. In this case, the flow rate profile is plug shaped, i.e. most particles move at approximately the same speed – only the particles in the direct vicinity of the wall move at a lower speed due to friction. As shown in Fig. 1.8a, the spectrum analyser in this case displays a narrow-band frequency curve. Low speeds are underrepresented, particularly during the systolic phase, and the so-called systolic window appears, i.e. an almost dot-free area below the ends of the curve envelope. The dots representing the higher speeds are particularly intense on the display.


Fig. 1.8
(a) Frequency spectrum of an undisturbed laminar flow. (b) Frequency spectrum of a turbulent flow
Sometimes, particularly when higher speeds are displayed on the screen due to stenosis, the laminar nature of the blood flow can be substantially disrupted. In this case, the particles no longer move along straight parallel paths but change their paths and speeds; sometimes, eddies and other disturbances occur. Since this type of turbulent flow produces many different speeds simultaneously, the Doppler spectrum appears as a broad band during the systolic phase, and the curve between the zero line and the peak value is relatively uniformly filled with dots (Fell et al. 1981) (Fig. 1.8b). Components of the flow moving in opposite directions as they occur inside the eddies appear below the zero line on the Doppler spectrum.
Since the amplitude of the curve on the spectrum is exactly proportional to the actual peak velocity, this method makes it possible to carry out at least semi-quantitative evaluations, in order to calculate and use indexes, for example. The Resistance Index according to Pourcelot (Planiol and Pourcelot 1973) has proved particularly effective for most applications. This index makes it possible to draw conclusions about the perfusion resistance downstream of the measurement site by comparing the height of the systolic peak flow velocity with the end-diastolic peak flow velocity. The equation is as follows:
 where ‘S’ is the systolic peak frequency and ‘D’ is the highest end-diastolic frequency.
where ‘S’ is the systolic peak frequency and ‘D’ is the highest end-diastolic frequency.

Figure 1.9a shows typical flow-velocity curves as a function of the subsequent perfusion resistance and the RI calculation. A low peripheral resistance is accompanied by a high diastolic amplitude and low RI. On the other hand, a high peripheral resistance is characterised by low diastolic amplitude and a high RI (Fig. 1.9b).


Fig. 1.9
(a) Schematic flow curve of a vessel supplying an area with low perfusion resistance. (b) Schematic flow curve of a vessel supplying an area with high perfusion resistance
Modern Doppler systems can detect the relevant measurement points S and D automatically and display the index on the screen in real time.
One alternative to the Resistance Index is the somewhat more complex Pulsatility Index of Gosling (Gosling and King 1974; Gosling et al. 1971). In contrast to the RI, this index not only detects the systolic and the end-diastolic peak but also takes into account the entire curve for the cardiac cycle, including any retrograde flow components which may be present. The peak-to-peak frequency must also be determined, i.e. the difference between the maximum and minimum frequency, where the minimum may also lie below the zero line in the case of an early diastolic retrograde dip (Fig. 1.10). Furthermore, an average value for the envelope must be calculated over one cardiac cycle – and this requires an electronic calculation.


Fig. 1.10
Measuring points for calculation of the pulsatility index
The Pulsatility Index is produced from the ratio of the peak-to-peak value to the average value.


Note: Some ultrasound systems offer different algorithms for determining the average value, e.g. by recording the integral, i.e. of all the frequencies beneath the envelope curve (TAM – time-averaged mean frequency). The PI values determined using these algorithms do not correspond to the measurement results based on the envelope curves. This must be taken into consideration during the evaluation and when comparing with the standard values.
1.4 Angle Problem
As already explained above and shown by the Doppler equation, a proportional relationship exists between the blood velocity and the Doppler frequency or the curve amplitude on the screen. However, this proportionality does not allow the determined Doppler frequency to be converted directly into the absolute blood velocity in m/s or cm/s.
This is due to the strong dependence of the Doppler frequency on the angle between the ultrasound beam and the direction in which the reflectors move. It is not the absolute speed of a reflector which is crucial for the development and intensity of the Doppler effect, but the velocity at which the distance between the reflector and the Doppler scan head changes. The difference between the absolute and detected velocity is illustrated in Fig. 1.11. While the erythrocyte moves at 1 cm per second in relation to its environment, its change in distance to the Doppler probe is smaller. For example, if the initial distance is 10 cm, the final distance after 1 s is only reduced to 9.3 cm. Therefore, from the point of view of the Doppler scan head, the approach velocity of the erythrocyte is merely 0.7 cm/s which means that the measured velocity is 30 % less than the actual velocity.


Fig. 1.11
Difference between true velocity and approach velocity
The angle between the direction of movement and the direction of observation is crucial for the difference between the measured velocity and the actual velocity – the wider the angle, the greater the discrepancy between the actual forward movement and the measured approach velocity (Fig. 1.12).


Fig. 1.12
Angle dependency of the Doppler frequency
With angles up to approximately 20°, the discrepancy is small and the detected Doppler frequency only deviates a little from the value which would be attained under the ideal conditions of 0°.
The deviation is calculated very easily from the cosine of the angle. At 0° (when the erythrocytes move directly towards or away from the probe), the cosine = 1 so that the genuine frequency shift occurs according to Doppler’s equation. At an angle of 15°, the cosine decreases to 0.97. Since this value enters the Doppler equation as a multiplication factor, the Doppler frequency which occurs drops to 97 % of the original value. The corresponding measurement error of 3 % can of course be disregarded. Even at 30° and a corresponding cosine of 0.87, the deviation amounts to a tolerable 13 % and is therefore still within the usual biological scatter of Doppler sonographic standard values. At 45°, the error increases to 25 % and at 60°, to a significant 50 % rising quickly as the angle widens. At 75°, the cosine is only 0.26 and the Doppler frequency detected by the equipment is therefore only 26 % of the frequency which would be produced under the optimum angle conditions. As the angle increases further to 90°, the cosine finally decreases to the value ‘0’, so the Doppler frequency detected is only 0 % of the optimum value. The erythrocytes pass under the ultrasonic beam at right angles so they neither approach nor move away from the probe and no longer give rise to a Doppler effect. The spectral display on the screen usually only shows weak interference signals in the region of the zero line, and the Doppler signals which are heard are mainly caused by movements of the vessel wall.
As the matters discussed previously show, the examining physician should always endeavour to obtain an acute-angled beam of the target vessel and place the probe accordingly in order to produce the optimum signal. Experts largely agree that angles wider than 60° cannot be relied on to produce a sufficiently large Doppler shift and the frequency spectra they produce should not be assessed. If the angle which can be obtained is between 30° and 60° due to the anatomical conditions, the question how to continue the procedure depends on the objective of the examination and must be determined by the following criteria:

With a purely qualitative evaluation of the frequency spectrum, particularly when the Resistance or the Pulsatility Index is used for the evaluation, the differences in frequency caused by the angle are immaterial since the systolic peak frequency is falsified to the same degree as the diastolic peak. The frequency spectrum displayed can therefore be used for the evaluation without further measures.
On the other hand, if the aim is to acquire a quantitative measurement of the flow velocity, the angle between the ultrasonic beam and the axis of flow must be known so that the cosine of this angle can be used for conversion into m/s or cm/s.

Because Doppler and B-mode imaging sonography are normally used in combination today, the angle can be seen directly on the screen by manually adjusting the angle cursor along the direction of flow visualised by the B-mode sonography. The system computer therefore receives the necessary information about the angle between the ultrasound beam and the axis of flow, determines the cosine automatically and takes this value into account when outputting the data and scaling the Doppler curve (see also the Sect. 1.6, Fig. 1.20).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree